
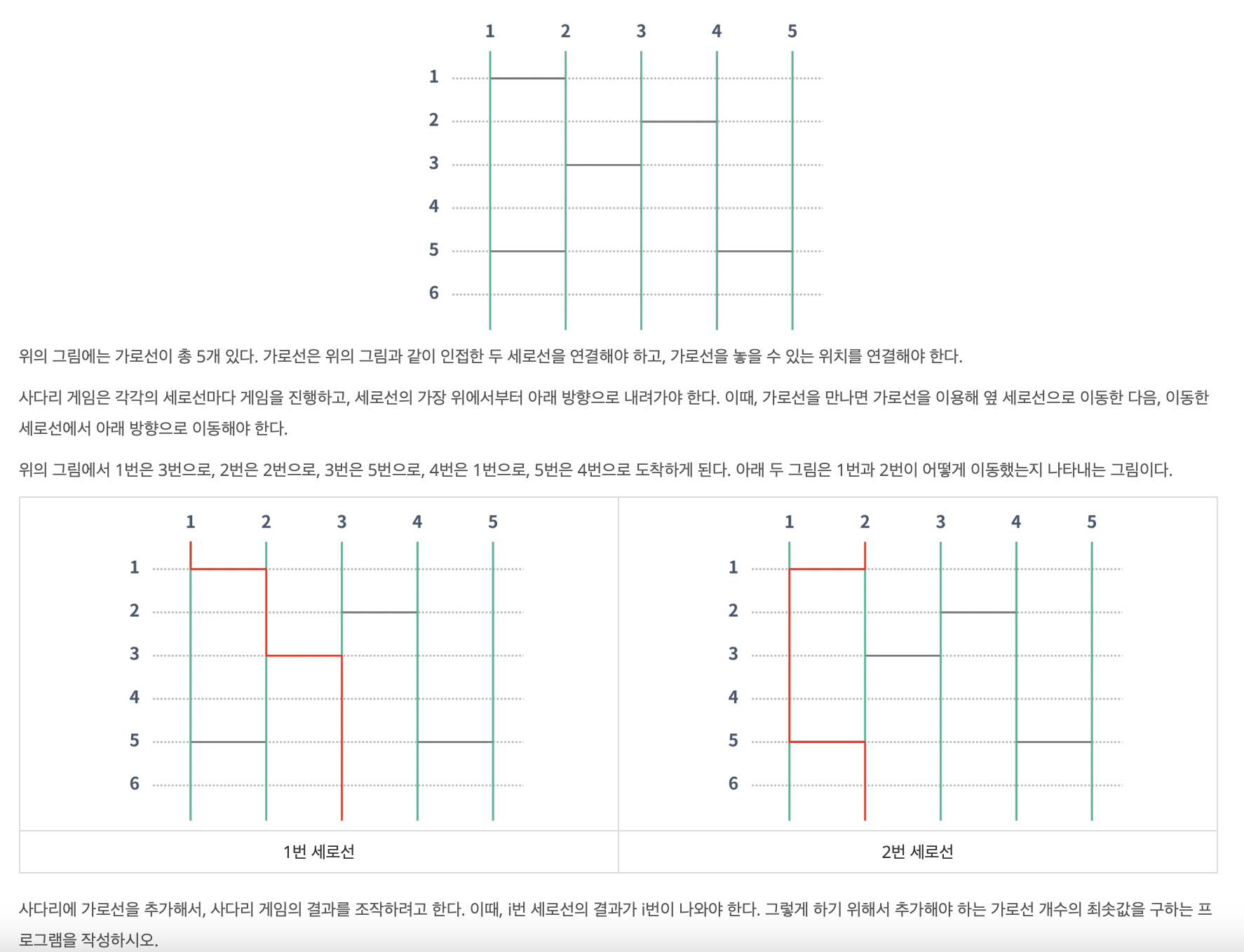
i 번 세로선의 사다리 게임 결과가 i가 되게 하기 위해 최대 3개의 가로선을 추가할 수 있다고 할 때 백트래킹을 이용하여 모든 경우를 완전탐색하는 문제이다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
|
#include<iostream>
using namespace std;
int N, M, H;
bool ladder[31][11];
int add;
bool finish;
void dfs( cnt)
{
if (finish)
return;
if (add == cnt) //몇개의 사다리를 추가했는지
{
bool flag = true;
for(int i=1; i<=N; i++)
{
int col = i;
for(int j=1; j<=H; j++)
{
if (ladder[j][col])
col++;
else if (col > 1 && ladder[j][col - 1])
col--;
}
if (i != col)
{
flag = false;
break;
}
}
if (flag)
finish = true;
return;
// i 번째 세로선에서 출발하여 i로 도착하는지 확인한다.
}
for(int i = 1; i <= H; i++)
{
for(int j=1; j<N; j++)
{
if (!ladder[i][j - 1] && !ladder[i][j] && !ladder[i][j + 1])
{
ladder[i][j] = true; // 사다리 추가하고
dfs( cnt + 1); // backtracking
ladder[i][j] =false; // 사다리 빼기
}
}
}
return;
}
int main()
{
cin.tie(NULL);
ios_base::sync_with_stdio(false);
cin >> N >> M >> H;
for(int i=0; i < M; i++)
{
int x, y;
cin >> x >> y;
ladder[x][y] = true;
} //사다리 셋팅
for(int i=0; i<=3; i++)
{
add = i; // 가로선 i개를 추가
dfs(0); // 백트래킹
if (finish)
{
cout << add << "\n";
return 0;
}
}
cout << -1 << "\n";
return 0;
}
|
cs |
저번 포스트에서 최솟값을 구하기 위해서는 BFS를 사용한다라는 말을 한적이 있었는데, 백트래킹을 이용하여도 최솟값부터 탐색할 수 있기 때문에 DFS로도 찾을 수 있다. 단, 문제에서 3개를 추가하는 경우까지 본다는 말은 depth를 3으로 제한한다는 말이다. 즉, 깊이가 깊어질수록 시간이 더 오래 걸릴 수 있기 때문에 BFS로 푸는 것이 좋다.
이 문제의 경우에는 백트래킹을 이용하여 전체 경우의 수를 다 탐색해야하므로 DFS로 풀었고, 핵심이 되는 로직은 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
for(int i = 1; i <= H; i++)
{
for(int j=1; j<N; j++)
{
if (!ladder[i][j - 1] && !ladder[i][j] && !ladder[i][j + 1])
{
ladder[i][j] = true; // 사다리 추가하고
dfs( cnt + 1); // backtracking
ladder[i][j] =false; // 사다리 빼기
}
}
}
|
cs |
i 번째 점선에서 j -> j +1로 가는 사다리를 추가하고 dfs 함수를 호출한 뒤(추가하였으므로 cnt + 1로 넘긴다.) 호출한 뒤 다음 사다리를 추가하기 위해서 ladder[i][j]에 false를 넣어줌으로써 다시 원상태로 돌려준다.
'Study > BOJ' 카테고리의 다른 글
| BOJ - 모노미노도미노 2 (0) | 2021.04.22 |
|---|---|
| BOJ - 구슬 탈출 2(13460) (0) | 2021.04.21 |
| BOJ - 어른 상어(19237) (0) | 2021.04.21 |
| BOJ - 행성 터널(2887) (0) | 2021.04.15 |
| BOJ - 다리 만들기 2(17472) (0) | 2021.04.15 |



